* 문제 링크
https://www.acmicpc.net/problem/3878
3878번: 점 분리
평면 위에 여러 개의 검정 점과 흰 점이 있다. 이때, 길이가 무한대인 직선을 그어 흰 점과 검은 점을 분리하려고 한다. 직선은 어떤 점과도 만나면 안 된다. 직선으로 인해서 나누어지는 두 그룹
www.acmicpc.net
문제 내용 요약
2차원 좌표 1사분면에 검정 점과 흰 점이 많이 있는데 (1 ≤ N,M ≤ 100)
얘네들을 직선 하나로 색깔별로 분리하려고 한다.
직선은 어떤 점도 만나면 안된다.
분리가 되는지 안 되는지 판단하자 (그림은 문제 링크 참고)
필요 배경 지식
두 가지 배경 지식이 필요하다.
컨벡스 헐과 선분 교차 판정 두 가지다.
이에 대한 기본적인 내용은 아래의 두 글을 참고하길 바란다.
컨벡스 헐 :
https://syerco0.tistory.com/10
백준 1708번 - 볼록 껍질
* 문제 링크 https://www.acmicpc.net/problem/1708 1708번: 볼록 껍질 첫째 줄에 점의 개수 N(3 ≤ N ≤ 100,000)이 주어진다. 둘째 줄부터 N개의 줄에 걸쳐 각 점의 x좌표와 y좌표가 빈 칸을 사이에 두고 주어진다
syerco0.tistory.com
선분 교차 판정 :
https://syerco0.tistory.com/16
백준 17387번 - 선분 교차 2
* 문제 링크 https://www.acmicpc.net/problem/17387 17387번: 선분 교차 2 첫째 줄에 L1의 양 끝 점 x1, y1, x2, y2가, 둘째 줄에 L2의 양 끝 점 x3, y3, x4, y4가 주어진다. www.acmicpc.net 문제 내용 요약 두 선분의 각 끝
syerco0.tistory.com
접근법
좌표 위의 점들이 하나의 직선으로 분리되려면 어떤 형태여야 하는가?
각 점들을 두 그룹으로 묶어서 생각했을 때,
각 그룹에 다른 색의 점이 들어가지 않는, 또는 두 그룹이 서로 겹치지 않는 경우에
일단은 분리되어있다고 생각할 수 있을 것이다.
 누가봐도 분리 안 됨 |
 일단은 분리가 되었는데... |
 분리도 되었고, 직선으로 분리 가능 |
검정과 흰색은 그림으로 표현하기 어려워 빨강과 파랑으로 표현했다.
1번 그림 빼고는 일단은 분리가 되었고, 3번은 누가 봐도 직선으로 분리가 된다.
2번 그림은 설명을 위해 어거지로 일단 표현했다.
점들을 분리할 수 있는 직선에 대해서,
같은 색깔의 점들을 이은 선분은 직선에 닿지 않을 것이며,
이 직선들을 모두 포함하는 가장 작은 다각형 또한 직선에 닿지 않을 것이다.
본인은 증명하기가 귀찮다. 하지만 직관적으로 그렇게 될 것임을 알 수 있다.
그런고로 배경 지식 부분을 보면 눈치챘겠지만, 컨벡스 헐 선에서 정리가 가능하다.

그럼 이제 컨벡스 헐을 구했으니, 두 개의 껍질이 분리되었는지만 확인해주면 된다.
별거는 없다. 껍질을 이루는 각 선분들이 모두 교차하지 않는지 확인해주면 된다.
각 색깔의 점들의 개수가 100개 이하이기 때문에, O(N^2)으로도 여유롭게 통과하니,
전체를 다 검사해주자.
그러면 해결!!........ 이 아니다.
점은 하나(점 하나로 구성)또는 두 개(선분 한 개로 구성)가 주어질 수 있기 때문에,
껍질을 구하지 못하는 경우의 예외를 처리해야 한다.
 점이 하나씩만 있으면 무조건 된다 |
 점 하나짜리를 선으로 가정해서 교차 판정을 해준다. |
 선분 교차 판정으로 해주면 된다. |
1. 점이 하나씩만 있는 경우, 무조건 직선으로 분리가 가능하다 (모든 점의 위치가 다르므로)
2. 각각 1개, 2개로 이루어진 경우, 1개짜리 점을 길이가 0인 선분으로 가정해서 선분 교차 판정을 해준다.
3. 2개씩 이루어진 경우, 선분 교차 판정을 해준다.
적당히 예외 처리를 해주면 된다.
이제 진짜 해결!!!!.......... 도 아니다.
생각해보면 선분 교차 판정을 하는 과정에서 맹점이 하나 있다는 것을 알 수 있다.
껍질 안에 껍질이 존재하는 경우다.

이러한 케이스를 걸러주기 위해서, 다른 색깔의 점이 껍질 내부에 존재하는지를 확인해주어야 한다.
컨벡스 헐을 구하는 과정에서 우리는 CCW 를 이용했고, 이에 따라 선분이 뻗어나간 방향이 있다는 것을 알고 있다.

각 빨간 선분을 기준으로 내부의 파란 점이 어디에 위치해 있는가?
왼쪽 방향에 위치해 있다는 것을 일단 직관적으로 알 수 있다.
CCW 로 생각해보면 어떤가? CCW = 1 이 됨을 알 수 있다.
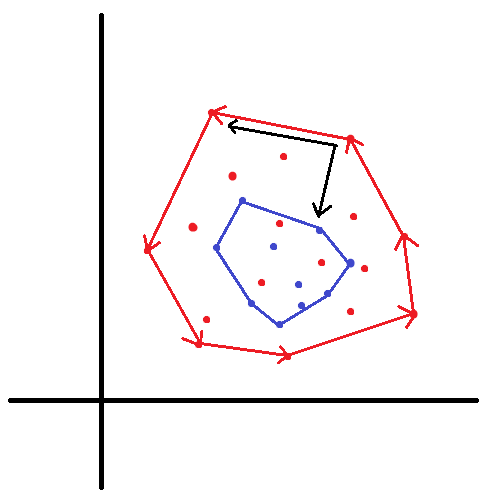
어차피 하나의 다른 색 점이라도 껍질 내부에 있으면 직선으로 분리가 불가하기 때문에,
각 색깔의 껍질에 대해 다른 색 점 하나의 위치만 확인해서 내부에 존재하는 형태를 걸러주면 된다.
최종적으로 선분 교차 판정을 통한 O(N^2) 의 시간 복잡도를 가지게 된다.
내 코드
#include <iostream>
#include <algorithm>
using namespace std;
struct D{
int x,y;
};
D nd[105],md[105];
int nmnm=0;
int ccw(D a,D b,D c) {
int n=(b.x-a.x)*(c.y-a.y)-(b.y-a.y)*(c.x-a.x);
if(n>0) return 1;
if(n<0) return -1;
return 0;
}
bool cmp(D a,D b) {
int n=ccw((nmnm==0?nd[0]:md[0]),a,b);
if(n==0) return a.x+a.y<b.x+b.y;
if(n>0) return 1;
return 0;
}
int big(D a,D b) {
if(a.y==b.y) return a.x>b.x?1:0;
return a.y>b.y?1:0;
}
bool intersect(D a,D b,D x,D y) {
int ccwa=ccw(a,b,x)*ccw(a,b,y);
int ccwb=ccw(x,y,a)*ccw(x,y,b);
if(ccwa==0&&ccwb==0) {
if(big(a,b)>0) swap(a,b);
if(big(x,y)>0) swap(x,y);
return big(b,x)>0&&big(y,a)>0;
}
return ccwa<=0&&ccwb<=0;
}
int main() {
int t;
cin>>t;
while(t--) {
int n,m,idx;
D nm={99999,99999},mm={99999,99999},ns[105],ms[105];
scanf("%d %d",&n,&m);
nmnm=0;
for(int i=0;i<n;i++) {
scanf("%d %d",&nd[i].x,&nd[i].y);
if(nm.y>nd[i].y||(nm.y==nd[i].y&&nm.x>nd[i].x)) nm={nd[i].x,nd[i].y},idx=i;
}
swap(nd[0],nd[idx]);
sort(nd+1,nd+n,cmp);
ns[0]=nd[0];
idx=1;
if(n>1) {
ns[1]=nd[1];
idx=2;
}
for(int i=2;i<n;i++) {
while(idx>1&&ccw(ns[idx-2],ns[idx-1],nd[i])<=0) idx--;
ns[idx++]=nd[i];
}
ns[idx]=ns[0];
n=idx;
nmnm=1;
for(int i=0;i<m;i++) {
scanf("%d %d",&md[i].x,&md[i].y);
if(mm.y>md[i].y||(mm.y==md[i].y&&mm.x>md[i].x)) mm={md[i].x,md[i].y},idx=i;
}
swap(md[0],md[idx]);
sort(md+1,md+m,cmp);
ms[0]=md[0];
idx=1;
if(m>1) {
ms[1]=md[1];
idx=2;
}
for(int i=2;i<m;i++) {
while(idx>1&&ccw(ms[idx-2],ms[idx-1],md[i])<=0) idx--;
ms[idx++]=md[i];
}
ms[idx]=ms[0];
m=idx;
if(n==1&&m==1) {
printf("YES\n");
continue;
}
int itst=0;
for(int i=0;i<n;i++) {
for(int j=0;j<m;j++) {
if(intersect(ns[i],ns[i+1],ms[j],ms[j+1])==1) {
itst=1;
break;
}
}
if(itst==1) break;
}
if(n>2) {
int ok=0;
for(int i=0;i<n;i++) if(ccw(ns[i],ns[i+1],ms[0])!=1) ok=1;
if(ok==0) itst=1;
}
if(m>2) {
int ok=0;
for(int i=0;i<m;i++) if(ccw(ms[i],ms[i+1],ns[0])!=1) ok=1;
if(ok==0) itst=1;
}
if(itst==1) printf("NO\n");
else printf("YES\n");
}
}
메모리 최적화를 귀찮다고 포기한 느낌이 없잖아 있다.
여담
설날 기간 동안 놀고 먹느라 글을 못 썼다.
역시 명절엔 쉬는게 짱이여
'개발일지 > Problem Solving' 카테고리의 다른 글
| 백준 11376번 - 열혈강호 2 (0) | 2023.01.30 |
|---|---|
| 백준 11375번 - 열혈강호 (0) | 2023.01.29 |
| 백준 17387번 - 선분 교차 2 (0) | 2023.01.19 |
| 백준 3679번 - 단순 다각형 (2) | 2023.01.18 |
| 백준 7420번 - 맹독 방벽 (2) | 2023.01.17 |


