* 문제 링크
https://www.acmicpc.net/problem/17387
17387번: 선분 교차 2
첫째 줄에 L1의 양 끝 점 x1, y1, x2, y2가, 둘째 줄에 L2의 양 끝 점 x3, y3, x4, y4가 주어진다.
www.acmicpc.net
문제 내용 요약
두 선분의 각 끝 점들이 주어지면 (그래서 점 2개씩 2개, 총 4개)
그 선분들이 교차하면 1, 아니면 0 을 출력해라
접근법
선분 교차 판정 문제는 CCW를 이용해서 푼다.
CCW에 대한 설명은 아래 글의 CCW 부분을 참고하길 바란다.
https://syerco0.tistory.com/10
백준 1708번 - 볼록 껍질
* 문제 링크 https://www.acmicpc.net/problem/1708 1708번: 볼록 껍질 첫째 줄에 점의 개수 N(3 ≤ N ≤ 100,000)이 주어진다. 둘째 줄부터 N개의 줄에 걸쳐 각 점의 x좌표와 y좌표가 빈 칸을 사이에 두고 주어진다
syerco0.tistory.com
뭔가 배움의 순서가 이상하게 되었지만, 과거부터 블로그를 시작하지 않은 나를 탓하자
일단 가장 일반적인 형태의 겹치는 모습을 보자

위에서 CCW를 읽고 왔으면 얼추 보일지 모르겠다.
빨간 점 2개와 각 파란색 점 하나씩해서 2가지의 CCW 를 구하면 어떻게 될까?
한 파란점은 반시계 방향, 나머지 하나는 시계 방향에 있어 CCW의 부호가 반대일 것이다.
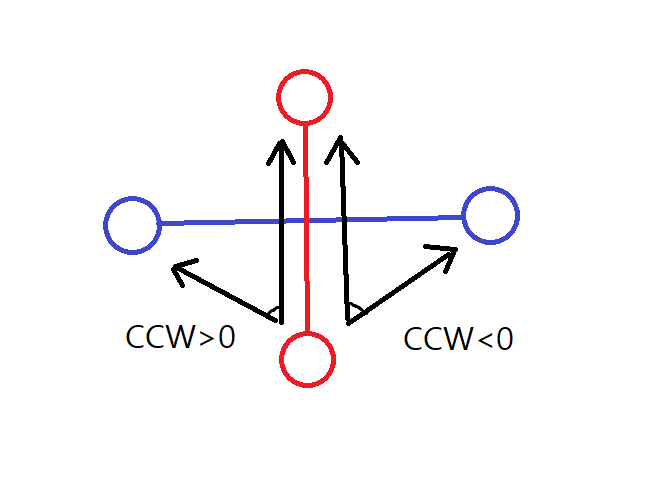
이번엔 파란 점 2개와 각 빨간점 하나씩 가지고 구해보자.

같은 색끼리는 순서가 달라도 어차피 두 개의 CCW 부호가 다를 것이라 상관이 없다.
그렇다면 대충 알겠는가?
한 선분의 점 2개를 기준으로 다른 선분의 점 하나씩과 CCW를 구했을 때, 부호가 달라야 한다.

물론 위의 그림처럼 CCW=0 이 되어도 한 점에서 만날 수 있기 때문에, 고려해줘야 한다.
줄이자면, 1,2번 점이 한 선분, 3,4번 점이 한 선분을 이뤘을 때,
CCWA = CCW(1,2,3) * CCW(1,2,4) ≤ 0 "AND"
CCWB = CCW(3,4,1) * CCW(3,4,2) ≤ 0
을 만족하면 "일반적인 상황"에서 선분이 교차를 하게 된다.
일반적으로 교차하지 않는 경우
CCWA = CCW(1,2,3) * CCW(1,2,4) > 0 "OR"
CCWB = CCW(3,4,1) * CCW(3,4,2) > 0
반대되는 경우도 한 번 보자.
 CCWA < 0 |
 CCWB > 0 |
보다시피 CCWB > 0 가 되어 선분이 교차하지 않음을 알 수 있다.
그러면 이제 "일반적인 상황"이 아닌 경우를 보자.
 |
 |
 |
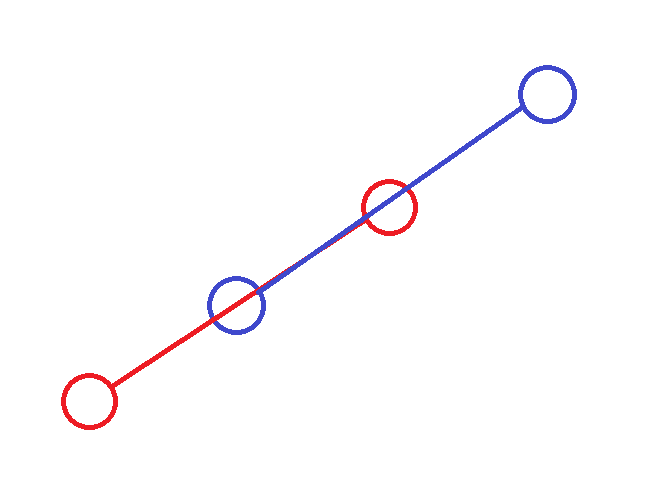
위의 경우는 CCWA=CCWB=0 중에서도, 네 점이 모두 한 직선 위에 있는 경우다.
이 경우에 선분이 1번 그림처럼 교차하지 않을 수도, 2,3번 그림처럼 교차할 수도 있다.
어떻게 구분할 것이냐....
(23.02.06 수정↓)
두 점을 비교했을 때 Y값, 같을 경우 X값이 더 크거나 같은 점을 bigDot(둘 다 같으면 둘 다 bigDot으로 판단),
다른 점을 smallDot 라고 하자 (작성자가 편한대로 정함)
각 선분 내의 두 점을 비교했을 때의 bigDot이 다른 선분의 smallDot와 비교했을 때에도 bigDot을 만족하면
두 선분은 교차한다.
그림으로도 간단하게 표현하겠다.
 |
 |
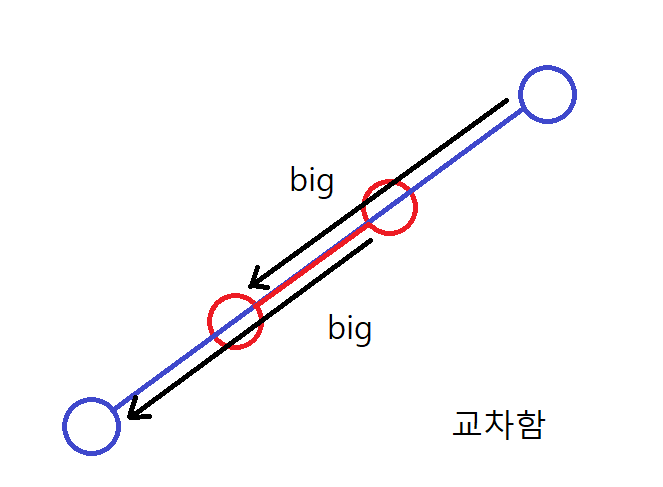 |
(23.02.06 추가 및 수정) 두 선분이 한 점을 공유할 때도 CCWA=CCWB=0 을 만족하는데,
이 경우에도 bigDot을 만족(같거나 크면 만족하도록 짰으므로)하여 교차한 것으로 판단하게되어 문제가 없다.
선분 교차 문제는 이렇게 해결된다.
처음 코드로 짜면 귀찮은 부분이 많지만
익숙해지면 괜찮아질 것이다.
내 코드
#include <iostream>
using namespace std;
struct dot{
long long int x,y;
};
struct line{
dot dots[2];
};
line l[2];
int bigDot(dot a,dot b) {
if(a.x==b.x) {
if(a.y==b.y) return 0;
return a.y>b.y?1:-1;
}
return a.x>b.x?1:-1;
}
int ccw(dot a,dot b,dot c) {
long long int res=(b.x-a.x)*(c.y-a.y)-(b.y-a.y)*(c.x-a.x);
if(res>0) return 1;
if(res==0) return 0;
else return -1;
}
int intersect(line a,line b) {
int ccwa=ccw(a.dots[0],a.dots[1],b.dots[0])*ccw(a.dots[0],a.dots[1],b.dots[1]);
int ccwb=ccw(b.dots[0],b.dots[1],a.dots[0])*ccw(b.dots[0],b.dots[1],a.dots[1]);
if(ccwa==0&&ccwb==0) {
if(bigDot(a.dots[0],a.dots[1])==1) swap(a.dots[0],a.dots[1]);
if(bigDot(b.dots[0],b.dots[1])==1) swap(b.dots[0],b.dots[1]);
return bigDot(a.dots[1],b.dots[0])>=0&&bigDot(b.dots[1],a.dots[0])>=0;
}
return ccwa<=0&&ccwb<=0;
}
int main()
{
int x[4],y[4];
for(int i=0;i<2;i++) {
scanf("%lld %lld %lld %lld",&l[i].dots[0].x,&l[i].dots[0].y,&l[i].dots[1].x,&l[i].dots[1].y);
}
cout<<intersect(l[0],l[1]);
return 0;
}
여담
사실 처음에 3878번 - 점 분리 문제를 올리려고 했으나
컨벡스 헐에 선분 교차 판정을 같이 쓰는 문제라
배경 지식용이자 3878번 설명 줄이기용으로 먼저 올렸다.
풀기는 되게 예전에 풀었다.
그리고 선분 교차1 문제도 있지만, 조금 더 케이스가 빡빡하지 않은 문제라
이거 풀면 금방 푼다 (순서가 반대로 되어버린)
선분 교차3도 풀기는 했었는데 더 귀찮고 어떻게 풀었는지 좀 까먹은 것 같다.
'개발일지 > Problem Solving' 카테고리의 다른 글
| 백준 11375번 - 열혈강호 (0) | 2023.01.29 |
|---|---|
| 백준 3878번 - 점 분리 (0) | 2023.01.24 |
| 백준 3679번 - 단순 다각형 (2) | 2023.01.18 |
| 백준 7420번 - 맹독 방벽 (2) | 2023.01.17 |
| 백준 1708번 - 볼록 껍질 (0) | 2023.01.03 |



